🤔 생각해볼 것
자료구조 트리에 대해서 설명할 수 있나요?
- 트리를 구성하는 요소와 명칭을 알고 있나요?
- 트리와 그래프의 차이를 설명할 수 있나요?
- 트리 순회 방법에는 무엇이 있나요?
이진트리에 대해서 설명할 수 있나요?
- 트리와 이진트리의 차이를 설명할 수 있나요?
- 이진 트리의 종류를 알고 있나요?
- 이진트리를 연결리스트를 이용하여 구현해보세요.
힙에 대해서 설명할 수 있나요?
이진 탐색 트리에 대해서 설명할 수 있나요?
- 힙과 이진 탐색 트리의 차이는 무엇일까요?
트라이에 대해서 설명할 수 있나요?
- 트라이를 이용해서 검색어 자동완성 기능을 구현해보세요.
트리(Tree)
트리는 하나의 뿌리에서 뻗어 나가는 형상처럼 생겨서 트리(나무)라는 명칭이 붙었다. 트리는 재귀적인 성격을 띈다. 트리는 부모 노드 밑에 여러 자식 노드가 연결되고 그 여러 자식 노드는 또 여러 자식 노드로 연결된다. 즉 트리는 트리(서브 트리)로 구성되어 있다. 트리는 HTML DOM, 파일 디렉토리 등에 사용되고 있다.

[1] 용어
1) 노드(Node) : 트리를 구성하는 원소를 노드라 지칭한다.
- 루트(Root) : 트리에서 부모가 없는 최상위 노드다. 트리는 항상 루트에서 시작한다.
- 부모 노드(Parent Node) : 루트 방향으로 직접 연결된 노드
- 자식 노드(Child Node) : 루트 반대 방향으로 직접 연결된 노드
- 형제(Sibling) : 같은 부모 노드를 갖는 노드
- 리프(Leaf) : 루트를 제외하고, 자식 노드가 없는 노드
2) 경로(Path) : 한 노드에서 다른 한 노드까지 이를 때, 거치는 노드의 순서 배열
3) 간선(Edge) : 부모 노드와 자식 노드가 직접 연결된 선을 지칭한다.
4) 길이(Length) : 한 노드(출발 노드)에서 다른 한 노드까지 거치는 간선의 개수
5) 레벨(Level) : 루트 노드의 레벨을 0이라 할 때, 루트 노드부터 어떤 노드까지 연결된 간선 수의 합
ex) 루트 노드의 자식 노드는 레벨이 1이고, 그 자식 노드는 레벨이 2이다.
- 높이(Height) : 루트의 레벨을 0 이라 할 때, 트리의 높이 값은 가장 깊은 레벨의 값과 같다.
6) 깊이(Depth) : 루트에서 어떤 노드까지의 길이
7) 차수(Degree) : 자식 노드의 개수
- 이진 트리의 차수는 2보다 클 수 없다.
- 트리의 차수 : 가장 차수가 큰 노드의 차수
8) 크기(Size) : 자기 자신을 포함한 모든 자식 노드들의 개수
9) 리프 노드(Leaf Node) : 자식을 갖지 않는 노드 = 차수가 0인 노드
[2] 특징
1) 노드가 N개인 트리는 반드시 N-1 개의 간선을 가진다.
2) 루트는 하나여야 한다.
3) 루트에서 특정한 정점으로 가는 경로의 개수는 반드시 1개이다.
4) Cycle이 발생하지 않아야 한다.
5) 부모노드에서 자식노드를 가리키는 단방향이어야 한다.
6) 자식 노드는 반드시 하나의 부모 노드를 가져야 한다.
7) 목적에 따라 다양한 트리 자료구조가 있다.
- 힙, 이진트리, 이진탐색트리, 인덱스 트리, 세그먼트 트리, AVL, 레드-블랙 트리, 트라이 등...
[3] 트리의 순회(order)
대표적으로 전위 순회, 중위 순회, 후위 순회가 있다.

이진 트리(Binary Tree)
$$이진트리 ⊂ 트리$$
기본적으로 트리의 형태를 떠올리면 이진트리 부터 떠올리는 경우가 많다. 이진트리는 트리의 한 종류이다. 이진트리의 경우, 자식 노드를 최대 2개만 가지도록 한다. 이유는, 자식 노드를 2개만 가지도록 했을 때 효율이 매우 뛰어나기 때문이다.
[1] 특징
1) 트리의 모든 노드의 차수가 2 이하라면, 그 트리는 이진트리라 부를 수 있다.
2) 정렬 여부와 관계 없이 모든 노드가 둘 이하의 자식을 갖는 단순한 트리 형태의 자료구조
3) 모든 부모 노드는 자식 노드를 최대 2개만 가질 수 있다는 점에서 데이터의 탐색 속도를 증진시킬 수 있다.
4) 정점이 N개인 이진트리는 최악의 경우 높이가 N이 될 수 있다. (편향 트리)
[2] 유형
이진 트리 중에서도 효율적인 트리 유형은 다음 3가지 유형이다.
(1) 정 이진트리
- 모든 노드가 0개 또는 2개의 자식 노드를 갖는다.
(2) 완전 이진 트리
- 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 모든 노드는 가장 왼쪽 부터 채워져 있다.
(3) 포화 이진 트리
- 모든 노드가 2개의 자식 노드를 가지고 있고, 모든 리프 노드가 동일한 깊이 또는 레벨을 갖는다.
- 가장 완벽한 유형의 트리
- 높이가 h인 포화 이진트리는 2^h - 1 개의 정점을 가진다.
이 3가지 유형의 트리 중에서 완전 이진 트리와 포화 이진 트리는 데이터의 구조가 많아도 시간복잡도가 현저히 줄어든다(logN). 부모 노드는 자식 노드를 최대 2개만 가질 수 있다. 이 점을 이용해서 트리를 배열로 구현하고, 인덱스 값을 통해 빠른 탐색을 할 수 있다.
힙(Heap)
1) 1964년 J.W.J. 윌리엄스(영국)가 힙 정렬을 고안해내며 설계한 자료구조
2) 완전이진트리 형태로 구현하고, 배열로 구현한다.
- 따라서 부모 노드와 자식 노드 간에 규칙(index)이 존재하고, 이러한 규칙 덕분에 매우 효율적인 자료구조.
3) 힙은 데이터 배열에서 최댓값(혹은 최솟값)을 찾기 위해 고안된 트리 자료구조이다. 따라서 힙의 특성(최대 힙 or 최소 힙)을 만족해야 한다.
- 최대 힙 : 부모가 항상 자식보다 크거나 같다.
- 최소 힙 : 부모가 항상 자식보다 작거나 같다.
4) 따라서 데이터 배열의 최댓값(혹은 최솟값)을 찾는 것에 목적을 둔다. 따라서 힙을 구현했다고 하여 힙 내부의 데이터들이 "정렬"된 것은 아니다.
5) 시간복잡도
- 힙은 값을 찾아내는 것만으로는 O(1)이다. 하지만 힙 내부적으로 데이터를 조정해주는 작업이 필요한데, 이 작업을 heapify라 한다. heapify의 시간복잡도는 완전 이진 트리의 특성 상 O(logN)이다. 따라서 힙의 삽입, 추출은 O(logN)이다.
5) 우선순위 큐 구현을 위한 자료구조이다. (결국 배열로 구현하는 셈)
여기서 잠깐 ! 우선순위 큐는 자료구조 일까요?
'우선순위 큐'는 '개념'이다.
우선 순위 큐를 구현하고 싶다면 힙 말고도 다른 여러 방법이 있을 것. 그래도 일반적으로는 힙으로 구현을 한다.
[1] Heapify
데이터를 힙으로 사용할 수 있도록 힙 내부를 조정하는 것을 말한다. 힙은 형제 노드의 값이 아닌 부모 노드와 자식 노드의 값만 비교한다. 최대힙의 경우 루트값이 max여야 하고 언제나 부모 노드 > 자식 노드 를 만족해야 한다.
예시) 데이터 배열 [7 6 5 8 3 5 9 1 6] 을 '최대 힙'으로 heapify하는 과정
배열을 순회하며 부모 노드 < 자식 노드라면 재귀적으로 교체한다.


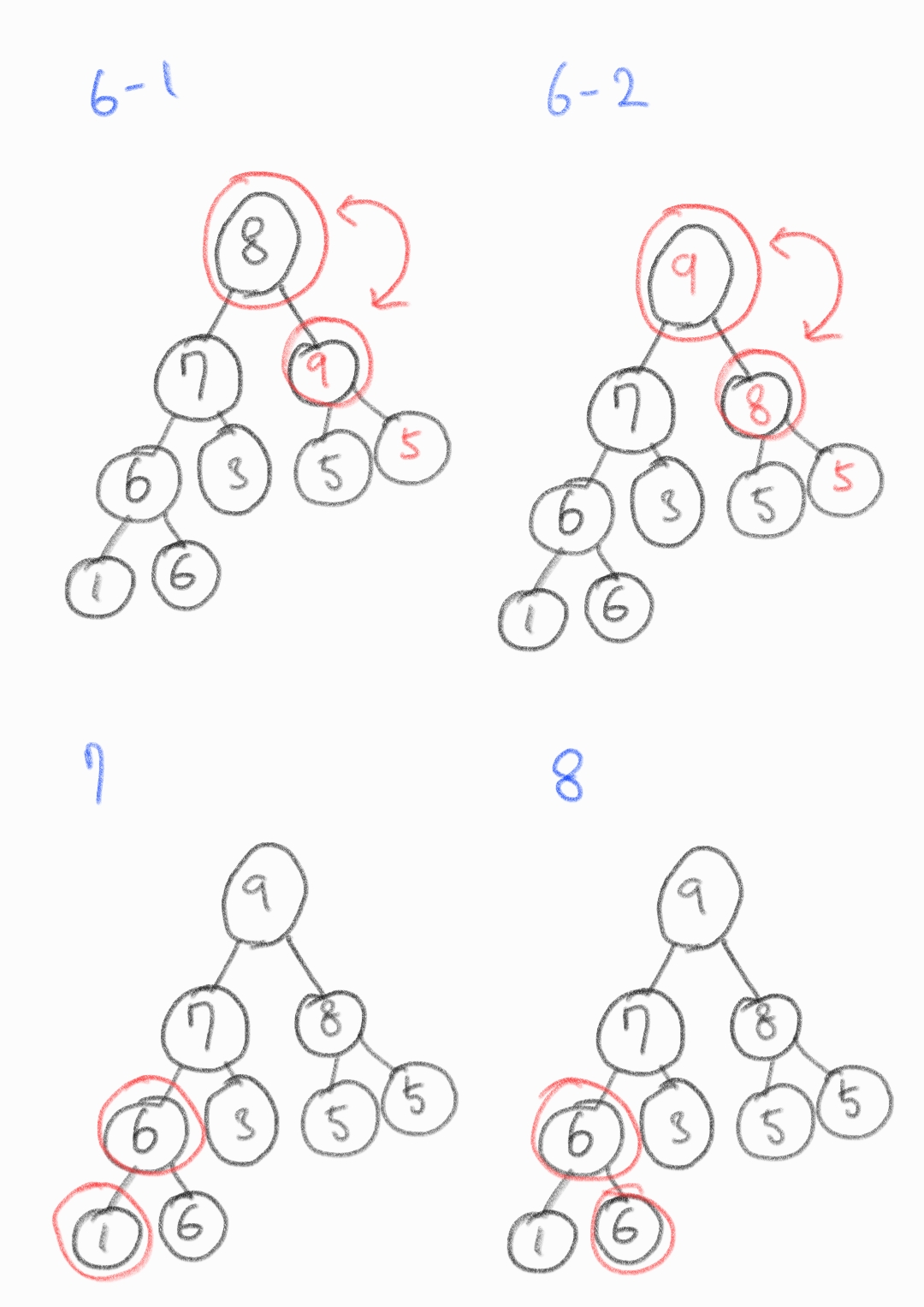
[2] 힙의 삽입과 추출
힙의 루트는 언제나 최댓값(혹은 최솟값) 이어야 한다. 따라서 추출 자체는 O(1)이지만, 추출한 뒤 힙 내부를 조정시키는 작업이 필요하다. 이 작업들은 O(logN)이 걸린다. 따라서 힙의 삽입과 추출은 O(logN)이다.
percolate-up
힙에 원소를 추가한 뒤 heapify하는 것. 힙은 완전 이진 트리로 구현하므로 삽입은 O(logN)이다.
(최대 힙이라면)
1. 트리의 가장 맨 마지막 요소로 추가한다.
2. 부모 정점보다 우선순위가 높다면 부모 정점과 위치를 스왑한다.
3. 2 과정을 재귀적으로 반복한다.
4. 3 과정이 끝났다면 현재 트리의 정점이 가장 높은 우선순위 정점이 된다.
percolate-down
(최대 힙이라면)
힙에서 원소를 추출한 후 heapify하는 것. 삽입과 마찬가지로 O(logN)이다.
1. root 정점을 삭제한다.
2. 트리의 가장 마지막 원소를 root에 넣는다.
3. root와 left, right 자식 노드를 비교해서 우선순위가 높은 노드와 스왑한다.
4. 3과정을 반복한다.
5. 4 과정이 끝났다면 삭제가 완료되었으니 1에서 삭제한 root를 반환한다.
이진 탐색 트리(Binary Search Tree)
힙과 이진 탐색 트리는 모두 완전 이진 트리로 구현을 합니다. 이 둘의 차이점은 무엇일까요?
그냥 이진 트리는 정렬 여부와 관계 없이 모든 노드가 둘 이하의 자식을 갖는 단순한 트리 형태였지만 BST는 정렬된 트리를 기반으로 한다.
부모노드를 기준으로 왼쪽에는 부모노드 값보다 작은 값이, 오른쪽에는 큰 값이 들어간다. 따라서 n개의 데이터 중 어떤 값을 찾기 위해서는 logN밖에 되지 않는 시간이 걸리기 때문에 매우 효율적이다.
[1] 자가 균형 이진 탐색 트리
하지만 루트노드부터 리프노드까지 한쪽 방향으로 쏠리는 트리의 불균형이 일어날 수 있기 때문에 트리의 균형을 맞추는 일이 매우 중요하다.
[2] 힙과 이진 탐색 트리
차이는 목적에 있다.
이진 탐색 트리는 원하는 데이터를 빠르게 찾고자 하는 것에 목적이 있다. 따라서 정렬된 데이터를 기반으로 한 이진 트리 자료구조로 구현한다. 이렇게 구현된 이진 탐색 트리는 이미 정렬이 되어있고, 이진 트리이기 때문에 탐색 시간복잡도가 O(logN)으로 매우 뛰어난 효율을 보여준다.
반면 힙은 항상 데이터의 최대, 최솟값을 찾는 것에만 집중한다. 따라서 힙 자체는 정렬된 상태가 아니다. 최대 힙으로 구성하고자 하여 힙을 생성했다면 항상 트리의 루트에는 데이터의 최댓값이, 최소 힙으로 구성했다면 최솟값이 존재한다. 따라서 이진 탐색트리에서는 부모 노드를 기준으로 더 작은 값은 왼쪽으로, 큰 값은 오른쪽에 위치시킨다. 반면 힙은 자식간의 대소관계는 신경쓰지 않고 부모와 자식의 대소관계만 중요하게 여긴다.
트라이(Trie)
[1] 특징
1) 전형적인 다진 트리
2) 탐색 트리의 일종으로, 문자열이나 연관 배열을 저장하는데 사용되는 트리 자료구조
3) 문자열 검색에 특화된 자료구조
4) 문자열 길이가 L일 경우 O(L)의 시간복잡도
5) 검색어 자동완성, 사전 찾기 등에 응용될 수 있다.
- 문자열의 길이가 L일때, 삽입은 O(L)
- 탐색 시간에 매우 효율적이다. 하지만 시간과 공간을 맞바꿨다. 메모리를 많이 사용하게 됨.
[2] 구조
1) root는 비어있다.
2) 간선은 추가될 문자를 key로 가진다.
3) 각 정점은 이전 정점의 값 + 간선의 key를 값으로 가진다.
4) 해시테이블과 연결리스트를 이용하여 구현할 수 있다.
📙 참고 도서
<파이썬 알고리즘 인터뷰> 박상길, 책만
🔗 참고 링크
트리
https://gmlwjd9405.github.io/2018/08/12/data-structure-tree.html
[자료구조] 트리(Tree)란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
https://jiwondh.github.io/2017/10/15/tree/
[Algorithm] 트리의 개념과 용어정리 | Jiwon Blog
트리의 개념과 용어정리
jiwondh.github.io
https://ko.wikipedia.org/wiki/%ED%8A%B8%EB%A6%AC_%EC%88%9C%ED%9A%8C
트리 순회 - 위키백과, 우리 모두의 백과사전
전산학에서 트리 순회(Tree traversal)는 트리 구조에서 각각의 노드를 정확히 한 번만, 체계적인 방법으로 방문하는 과정을 말한다. 이는 노드를 방문하는 순서에 따라 분류된다. 여기서 설명하는
ko.wikipedia.org
힙
https://ko.wikipedia.org/wiki/%ED%9E%99_(%EC%9E%90%EB%A3%8C_%EA%B5%AC%EC%A1%B0)
힙 (자료 구조) - 위키백과, 우리 모두의 백과사전
1부터 100까지의 정수를 저장한 최대 힙의 예시. 모든 부모노드들이 그 자식노드들보다 큰 값을 가진다. 힙(heap)은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리(com
ko.wikipedia.org
https://asfirstalways.tistory.com/325
[Sorting] 4. Heap, Heapify, Heap Sort
Heap Sort Space-Complexity = In-place sort : O(1)의 보조 메모리를 사용한다. Time-Complexity = O(n log n) 원리 heap 자료구조를 활용할 Sorting 방법에는 두 가지 방법이 존재한다. 하나는 정렬의 대상인..
asfirstalways.tistory.com
https://www.andrew.cmu.edu/course/15-121/lectures/Binary%20Heaps/heaps.html
Heaps
Binary Heaps Introduction A binary heap is a complete binary tree which satisfies the heap ordering property. The ordering can be one of two types: the min-heap property: the value of each node is greater than or equal to the value of its parent, with the
www.andrew.cmu.edu
💡 오늘의 회고
오늘은 트리 관련 자료구조만 공부했다. 사실 완전 처음 공부한 것은 아니고 예전에 자료구조를 혼자 공부하면서 정리했던 것들을 다시 펼치고 되짚어보며 다시 정리를 하였음. 점점 정리를 거칠 수록 글이 깔끔해지는 것 같기는 한데... 적는데 너무 오래 걸리는 것 같다. (이 부분을 어떻게 개선시켜야 하나... 더 집중하고 부지런해져야 하나...)
힙을 한번 구현해본 적은 있지만 이곳 저곳을 많이 참고하면서 구현했던 터라 직접 구현하려니 역시 어려웠다. 온라인 코딩테스트라면 미리 만든 힙 클래스를 사용하면 되겠지만 만약 나중에 라이브 코딩에서 힙을 구현하라 한다면...😨
이번에 다시 복습 차원에서 구현을 해봐야겠다.
트리는 알고 있지만 항상 용어가 헷갈림... 이것도 다시 리마인드했다. 트리 순회도 항상 헷갈리는 것 중 하나인데 다시 리마인드.
트라이는 여전히 어렵다.
이번 주는 거의 자료구조를 자바스크립트로 구현만 하고 있는데... 원래 글 정리하는 것이 느려서 TIL도 너무 오래 걸리는 것 같다. 조금 더 가볍게 써야 하나...? ㅠㅠ 뭔가 성격 상 그럴 수가 없다... 큐부터 코드를 하나하나 구현해야하는데 글을 적느라 거의 하나도 못했다. 내일은 주말이니까 불코(불타는 코딩이라는 뜻. 방금 그냥 지어냈음) 해야지 🔥 글 적는 것에는 오래 걸렸지만 역시 적고나니 뿌듯.
데브코스 1주차가 끝났읍니다. 간단소감? 그냥 너무 좋음!!! 👍👍
노션 블로그에 회고를 작성해보았읍니다.
https://ryong9rrr.notion.site/e6f894690dd94c5fa50bcae89fd0b3ec
데브코스 첫 주를 마치며
A new tool for teams & individuals that blends everyday work apps into one.
ryong9rrr.notion.site
'프로그래머스 데브코스' 카테고리의 다른 글
| [데브코스 7일차] 이진 탐색 + 1주차 회고 (0) | 2022.03.29 |
|---|---|
| [데브코스 6일차] 정렬 알고리즘 (0) | 2022.03.29 |
| [데브코스 4일차] 큐, 해시테이블, 그래프 (4) | 2022.03.24 |
| [데브코스 3일차] 자료구조와 알고리즘 (2) | 2022.03.24 |
| [데브코스 2일차] CS (0) | 2022.03.23 |



